研究実績

当研究室では，さまざまな計算モデルを例から学習するという問題を理論的に扱っている．
例えば，以下の図で表される決定性有限オートマトンを例から学習するという問題を考えよう．

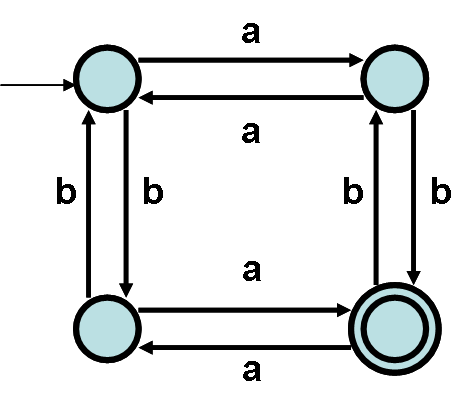
このオートマトンは，横方向に移動するときに記号 a の出現回数の偶奇性を判断し，上下方向に移動するときに記号 b の出現回数の偶奇性を判断する．
つまり，記号 a および b の出現回数がともに奇数であるときに，入力記号列 を受理する．
例からの学習では，以下の表のような受理されるべき記号列(正例という)の 有限データと， 受理すべきでない記号列(負例という)の有限データが与えられたときに， それに対応するオートマトンを求める問題を考える．

正例	負例
aabababa	aabbababaa
abbabbba	aababa
bbababab	babaabab
ba	bbaa
abbbaaaa	bb

のように，例から自動的にオートマトンを得ることができれば， オートマトンの理論を熟知していない人でも，例を与えることさえできればオートマトンを設計できることにつながる．

例の学習は，別の見方をすると，与えられたデータに潜む規則性を自動的に 計算機によって発見する問題を取扱っていると考えられる．
つまり，さまざまな 応用の可能性を秘めている．

本研究室で取扱っている学習対象として，以下のような計算モデルが挙げられる．

• オートマトン
• 文法（正則文法，文脈自由文法，木文法，など）
• 実数データを扱えるオートマトン
• 確率計算モデル

当研究室では，主に，核酸配列を代表とする生体高分子の構造解析に関するアルゴリズムの研究と応用を行っている．

生物の遺伝情報は基本的に DNA に格納されている．
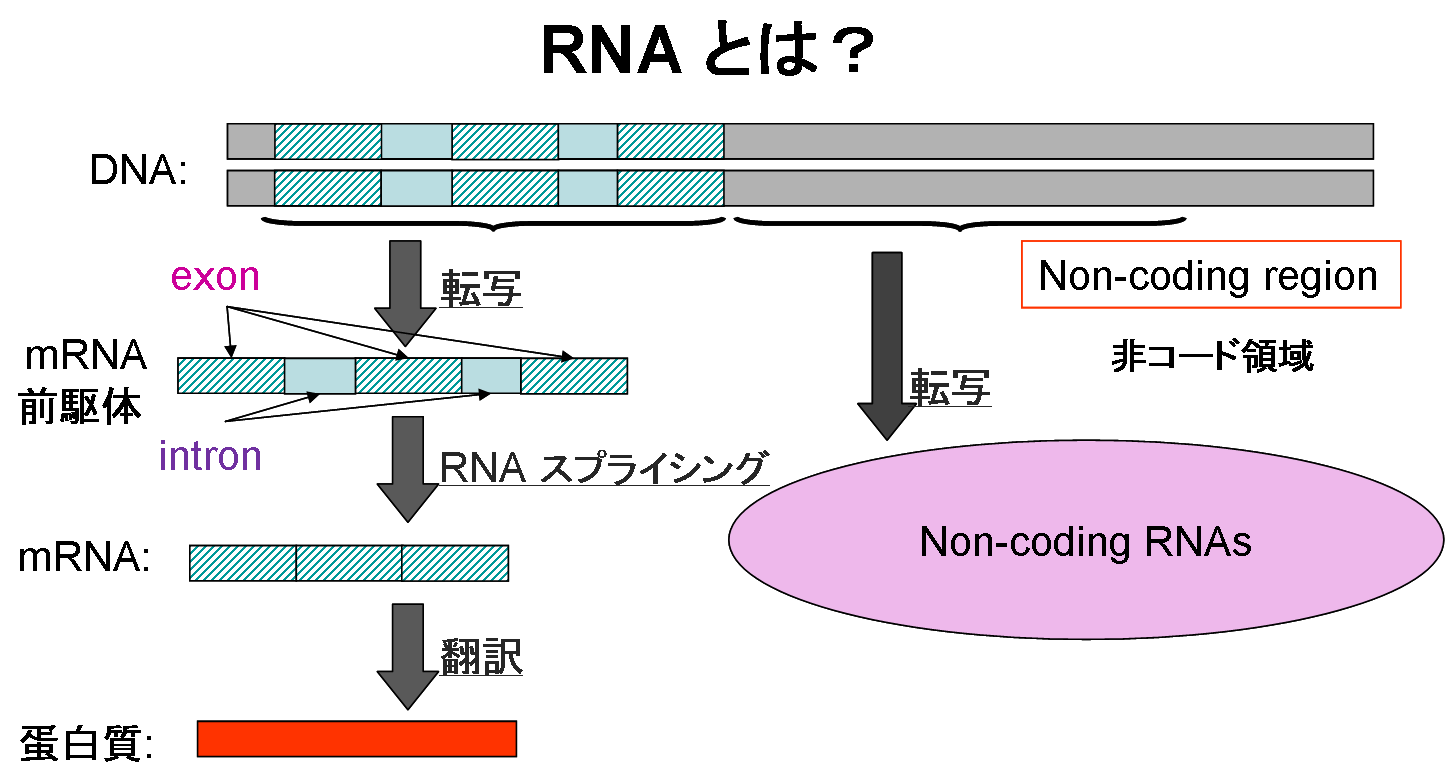
その情報は，まず mRNA 前駆体というRNA 分子に写しとられ(転写され)， スプライシングという余分な配列を除去するプロセスを経た後，mRNA が完成する．
そして，mRNA はリボゾームとよばれる分子の機械によって， 蛋白質に翻訳される．
しかしながら，近年，転写された後に翻訳の工程を経ずに RNA 分子としてさまざまな機能を持つものがたくさん存在することがわかってきた．
これらを総称して 非コードRNA(Non-coding RNA)という．

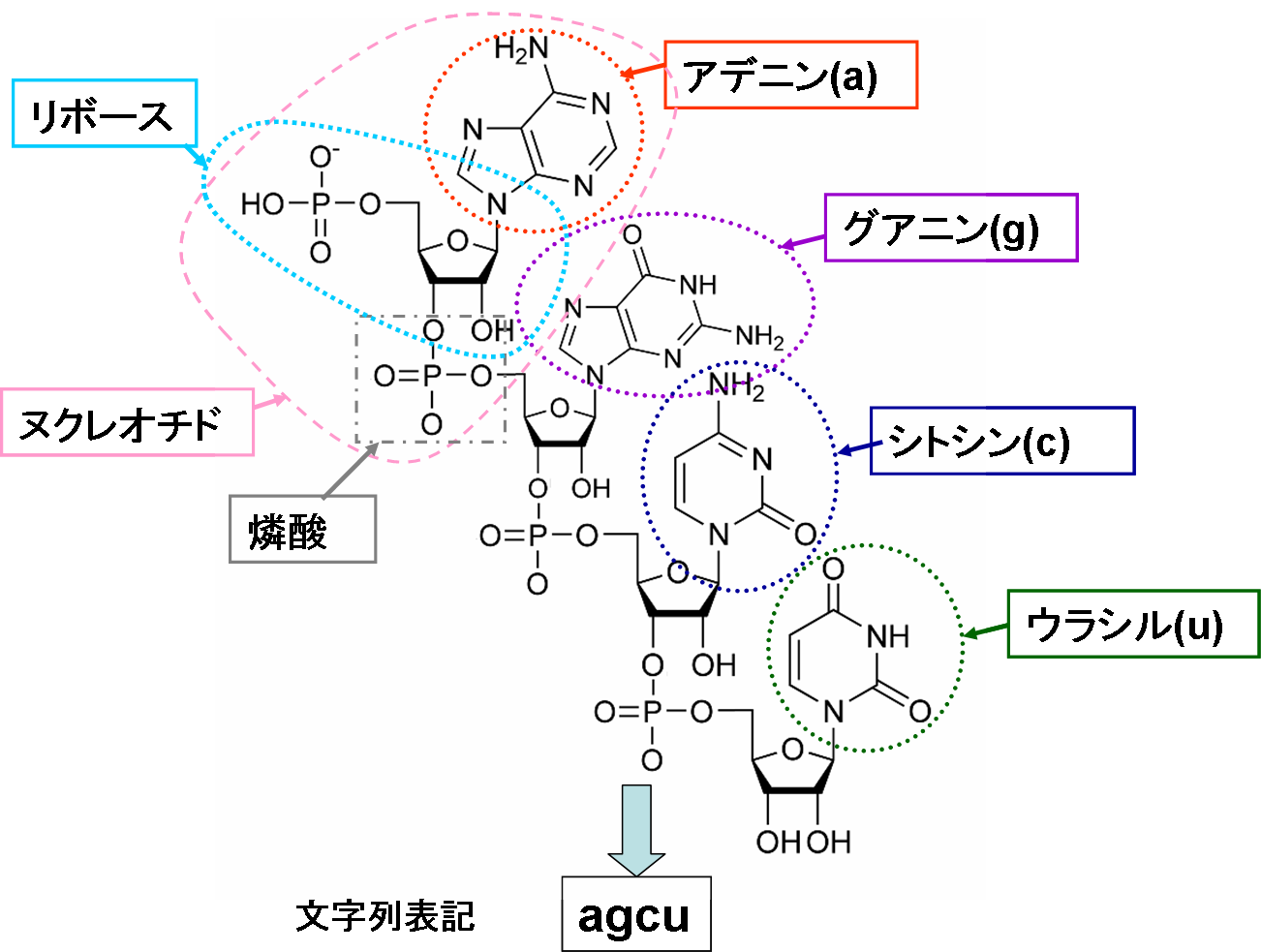
RNA はヌクレオチドが重合してできる一本鎖状の生体高分子であるが， アデニン(A)，グアニン(G)，シトシン(C)，ウラシル(U)の 4 種類の塩基を並べた文字列と考えることができる．(下図参照)

しかも，ワトソン・クリックの相補性に基づいて， A と U，および，C と G が水素結合して塩基対を形成するため， 下図のような二次構造をとることが知られている．

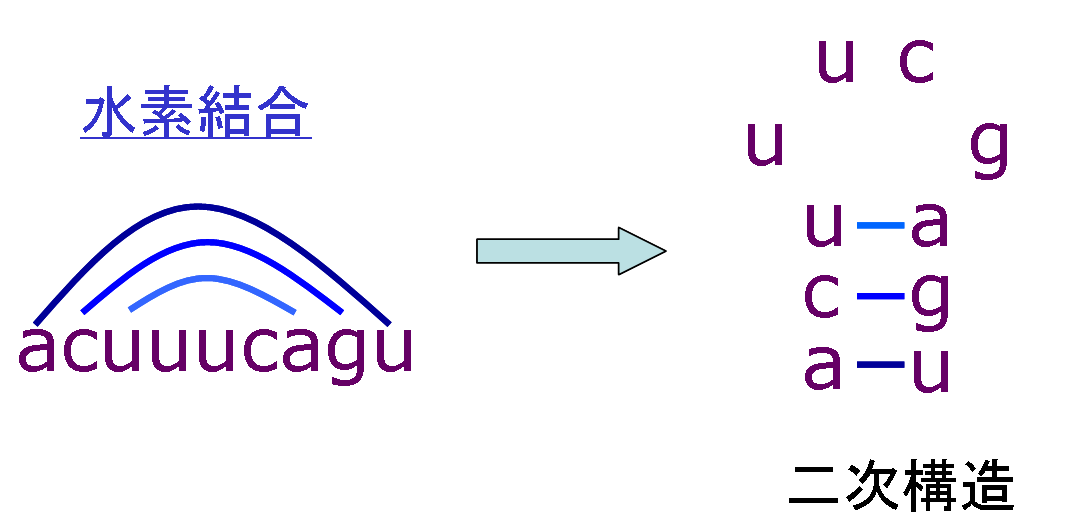
このような構造はＲＮＡの機能と密接に関係しており，二次構造を予測することができれば，その機能解明に役立つ．
当研究室では，このような核酸配列の二次構造レベルでの構造解析を行うためのアルゴリズムに関する研究を行っている．

このような構造はＲＮＡの機能と密接に関係しており，二次構造を予測することができれば，その機能解明に役立つ．
当研究室では，このような核酸配列の二次構造レベルでの構造解析を行うためのアルゴリズムに関する研究を行っている．

この問題の難しさは，このような二次構造の数が，配列の長さが増えるに従って組み合わせ爆発を起こすところにある．
特に，複数の核酸配列が干渉するような反応系を考えると，この組み合わせ爆発の問題はより深刻になる．
このような組み合わせ爆発の問題を打破するためのアルゴリズムに関する研究を進めている．

この研究テーマは， 分子に情報処理をさせようというかなり異端な研究テーマである．
この分野の発端は，1994 年に発表された Adleman の研究である．
Adleman は，NP 完全問題の1つであるハミルトンパス問題という グラフ問題を，DNA 分子に符号化して解く実験プロトコルを提案し， 実際にそれで解けることを分子生物学的実験で示した．
その後， 計算機科学，分子生物学，ナノテクノロジーなどの分野の研究者の興味を集め，地道に研究が進められている．

この研究分野は，現在のコンピュータより高速なものを作ることを目指しているわけではない．
分子に情報処理を行わせることが 有効であると思われるさまざまな分野(バイオテクノロジーやDNA ナノテクノロジー)に応用しようという視点で研究が進められている．

例えば，下図のように赤，青，緑，紫で表されている4本の DNA 配列で平面状のタイル構造を構築することができる．
図の点線で示される結合がワトソン・クリックの相補性に 基づく水素結合を示している．

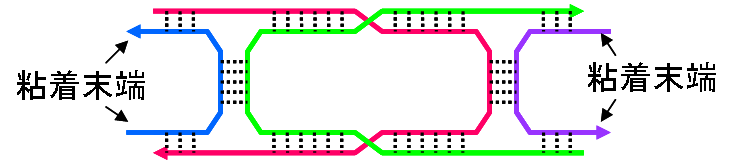
このような平面タイルの4隅に余分な DNA 配列を意図的に 残しておくと，その部分(粘着末端とよばれる)が糊の働きをして他のタイルと 結合してさらに大きな複合体を構成する(下図参照)．

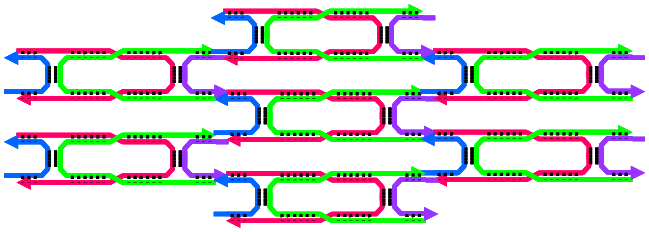
DNA ナノテクノロジーの分野では，このようなタイルを用いて 意図的な微細構造を自律的に形成させようとする研究がさかんに 行われている．
その際，意図的な構造を形成するには情報科学的な 発想が必須である．
例えば，上記のタイルを用いて，決められた辺の長さを もつ正方形を形成させたい場合を考えよう．

そのためには， 縦と横の両方向に決められた個数だけタイルを会合させる必要がある．
つまり，タイル自身が会合しながら会合したタイルの個数をカウント しなければならない．
これは，タイル自身が自律的に 計算を行う必要があることを物語っている．

また，当研究室では，このような分子に計算をさせるという研究をより発展させて，分子でロボットを創ろうという新しい研究プロジェクトにも参加している．
ロボットは，環境からセンサーを通して得た情報を，回路で変換してアクチュエータに伝えるというプロセスを繰り返して動作するシステムである．
当研究室が関わっているのは，分子ロボットの構築のために必要となる回路を分子計算によって実現する研究である．

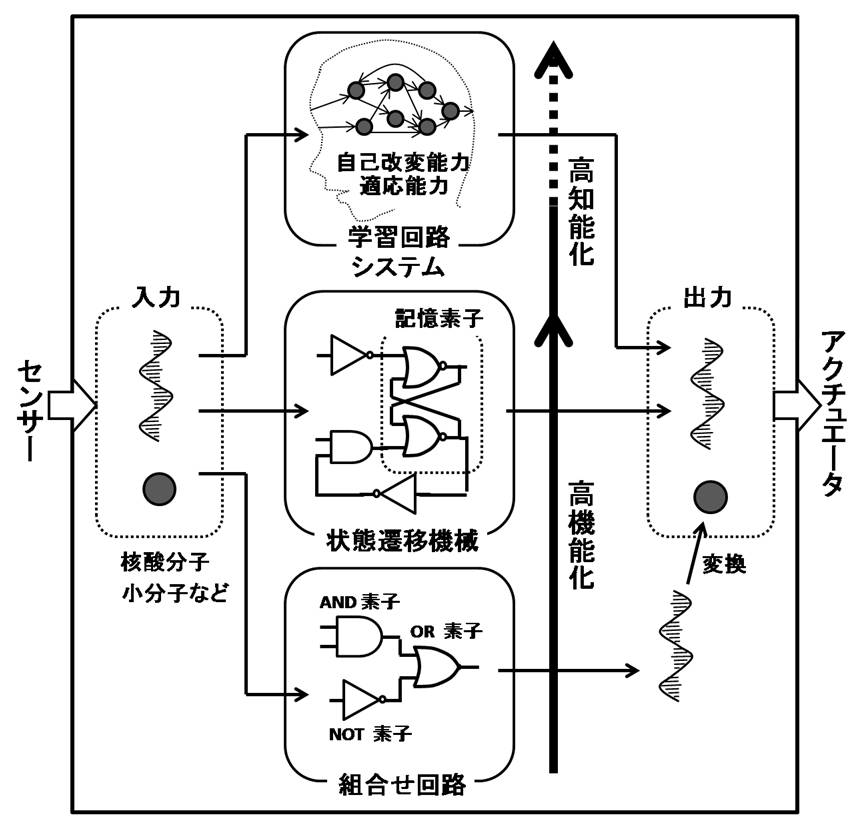
このような回路を核酸配列をベースとした化学反応系で実現し，より高度な知的機能をもつ分子ロボットをいつの日か構築できることを夢見ている．