研究プロジェクト

反応系の状態空間を「構造体の空間」と「濃度分布の空間」の２つの軸を設けて記述することにしたいと思います．
以下の図において，横軸には反応系で生成されるすべての構造体が概念的に記載されています．
縦軸は，各構造の濃度を表します．
このように軸をとると，反応系の構造体の濃度分布は，図の実曲線で描かれたグラフとして記述できます．

ここで，平衡状態を求める問題は，図で実曲線のグラフとして描かれているさまざまな濃度分布の中で，最小自由エネルギーをとる濃度分布を求める問題と理解できます．

従来の研究では，構造体の中で重要ではないと思われるものを除去して構造の爆発を回避するといった手法が取られることが主でした．
しかしながら，これでは，平衡状態を厳密に求めることはできませんし，近似的に求めることができたとしても，系の規模（生体高分子の長さなど）が大きくなるにつれて次元数が組み合わせ爆発することは防げません．
これに対して，本研究では，濃度分布の間に類似関係（数学的には同値関係）を導入し，類似した濃度分布（同値な濃度分布）どうしをひとつにまとめることによって次元数を削減するという新しいアプローチをとりました．

生体高分子のように複雑な構造を形成し得る分子が干渉し合う系は，反応系内で生成される構造の個数が極めて大きくなります．
類似関係（同値関係）をどのように定めるかは，グラフを用いて構造体を数え上げるという発想に集約されます．
ここで，２種類のタイル a, b が会合して１次元的に連なった集合体を形成する反応系を考えましょう．
例えば，aba は，a, b, a の順に左から右にタイルが並んだ１次元構造を表します．
ただし，この構造のギブス自由エネルギーは，タイルの接触のパターンによって局所的に決まるものと仮定します．
つまり，a の右隣に b が来る場合は，e(a,b)=-1.2 kcal/mol，b の右隣に a が来る場合は，e(b,a)=-2.5 kcal/mol といった具合です．
aba という構造に対しては，この局所的な自由エネルギーの総和である e(a,b)+e(b,a) = -3.7 kcal/mol が自由エネルギーとなります．
これは，本研究で開発した理論を適用する上での重要な仮定です．
一般的に述べると，

構造体の自由エネルギーは，その局所構造の自由エネルギーの総和として求められる

ということが仮定されています．
このような仮定は，核酸配列のような生体高分子を二次構造レベルで解析する場合によく用いられています．

ところで，上記のタイルの反応系では，長さ n の構造体の個数は，2 の n 乗個存在するので，系を記述するための変数は組み合わせ爆発を起こします．
そこで，本研究では，グラフを用いて構造体を数え上げるという発想を用います．
例えば以下のグラフを考えましょう．

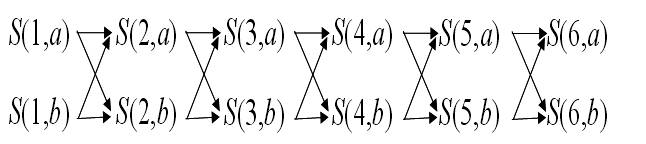
これは，長さ６のタイル構造をすべて数え上げるためのグラフです．
ここで，S(1,p) および S(6,p) といった形の頂点がそれぞれ初期頂点および最終頂点になります．
初期頂点から最終頂点へのパスとタイルの構造を対応させることにより，構造の数え上げを行います．
例えば，図においてS(1,a)→S(2,b)→S(3,a)→S(4,b)→S(5,b)→S(6,a)というパス α は，ababba というタイルアセンブリに対応します．
このように，グラフ上のパスと反応系の構造を対応させることにより数え上げを行います．

本研究では，このような数え上げを行うことにより，反応系の平衡状態を求めるのに必要な変数の個数がグラフの辺の個数で十分であることを示しました．
グラフの辺こ個数はパスの個数に比べて非常に小さいことにご注目下さい！
つまり，平衡状態の解析に必要な次元数を劇的に削減することに成功しました．

このようなグラフによる数え上げの発想は，単に平衡状態を求めるだけでなく，反応系の各構造物の濃度の時間変化の近似シミュレーションに応用できることがわかりました．
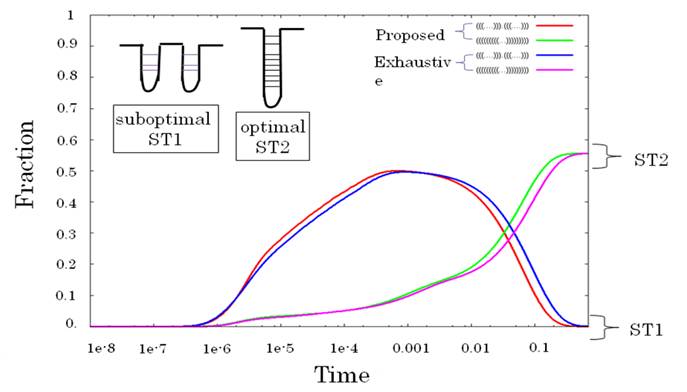
以下のグラフは，RNAのフォールディングの過程をシミュレーションすることに応用したものです．
Exhaustive とあるのが厳密なシミュレーションで，Proposed とあるのが本提案手法による近似シミュレーション結果です．
近似シミュレーションでもだいたいの挙動を説明できていることがわかると思います．
計算速度は提案手法の方が圧倒的に早く，長さが長くなるにつれてその効果は大きくなります．
実際，厳密にやろうとすると数時間かかるものが１０分程度で済むといった高速化が達成されています．

本研究では，このように極めて高次元の系に対して，次元数を削減するための一般的な方法論を展開しました．
その結果，極めて高速に平衡状態の解析や近似シミュレーションを実行できる技術を与えることに成功しました．